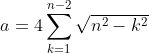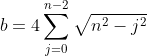2.4 KiB
2.4 KiB
Approximating Pi Using Numerical Summation
Explanation
This method approximates the value of \pi using a numerical summation technique. The approach is based on the concept of inscribing and circumscribing rectangles under a quarter-circle to estimate the area. By summing the areas of these rectangles, we can approximate the area of the quarter-circle, which in turn helps us estimate \pi.
Mathematical Representation
The equation used is:
Where:
aandbare summations that approximate the quarter-circle area.- The sum iterates over a set of discrete steps to refine the approximation.
More specifically, a and b are defined as:
Python Equivalent
import math
def approximate_pi(n=46325):
lange = n - 2
a, b = 0, 0
# Compute summation for 'a'
for k in range(1, lange + 1): # Changed to include lange
a += math.sqrt(n**2 - k**2)
# Compute summation for 'b'
for j in range(lange + 1): # Changed to include lange
b += math.sqrt(n**2 - j**2)
# Normalize the results
b = 4 / (n**2) * b
a = 4 / (n**2) * a
result = (a + b) / 2
return result
# Run the function
print(approximate_pi())
How It Works
- Initialization: The variable
langeis set ton - 2, and two summation variablesaandbare initialized to zero. - Summation for 'a': Iterates from 1 to
lange, calculating the square root ofn^2 - k^2for eachk. - Summation for 'b': Iterates from 0 to
lange, calculating the square root ofn^2 - j^2for eachj. - Normalization: Both summations are normalized by multiplying by
\frac{4}{n^2}. - Result Calculation: The final approximation of
\piis obtained by averaging the normalized values ofaandb.
Conclusion
This method provides an approximation of \pi using numerical summation. The accuracy increases as n grows larger, effectively refining the result. By adjusting the value of n, you can control the trade-off between computational effort and precision.
Notes
- The choice of
n = 46325is arbitrary and can be adjusted for better performance or higher precision. - This method is computationally intensive and may require optimization for very large values of
n.