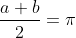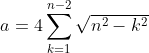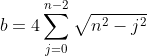fabelous-math/docs/pi.md

Approximating Pi Using Numerical Summation

Explanation

This method approximates the value of \pi using a numerical summation technique. The approach is based on the concept of inscribing and circumscribing rectangles under a quarter-circle to estimate the area. By summing the areas of these rectangles, we can approximate the area of the quarter-circle, which in turn helps us estimate \pi.

Mathematical Representation

The equation used is:

Where:

• a and b are summations that approximate the quarter-circle area.
• The sum iterates over a set of discrete steps to refine the approximation.

More specifically, a and b are defined as:

Python Equivalent

import math

def approximate_pi(n=46325):
    lange = n - 2
    a, b = 0, 0

    # Compute summation for 'a'
    for k in range(1, lange + 1):  # Changed to include lange
        a += math.sqrt(n**2 - k**2)

    # Compute summation for 'b'
    for j in range(lange + 1):  # Changed to include lange
        b += math.sqrt(n**2 - j**2)

    # Normalize the results
    b = 4 / (n**2) * b
    a = 4 / (n**2) * a
    result = (a + b) / 2

    return result

# Run the function
print(approximate_pi())

How It Works

1. Initialization: The variable lange is set to n - 2, and two summation variables a and b are initialized to zero.
2. Summation for 'a': Iterates from 1 to lange, calculating the square root of n^2 - k^2 for each k.
3. Summation for 'b': Iterates from 0 to lange, calculating the square root of n^2 - j^2 for each j.
4. Normalization: Both summations are normalized by multiplying by \frac{4}{n^2}.
5. Result Calculation: The final approximation of \pi is obtained by averaging the normalized values of a and b.

Conclusion

This method provides an approximation of \pi using numerical summation. The accuracy increases as n grows larger, effectively refining the result. By adjusting the value of n, you can control the trade-off between computational effort and precision.

Notes

• The choice of n = 46325 is arbitrary and can be adjusted for better performance or higher precision.
• This method is computationally intensive and may require optimization for very large values of n.