|
Gitea Actions For Fabelous-Math / Explore-Gitea-Actions (push) Successful in 18s
Details
|
||
|---|---|---|
| .gitea/workflows | ||
| .vscode | ||
| docs | ||
| src/fabelous_math | ||
| tests | ||
| .gitignore | ||
| LICENSE | ||
| README.md | ||
| example.py | ||
| pyproject.toml | ||
| pytest.ini | ||
| requirements-dev.txt | ||
| result.py | ||
| setup.py | ||
README.md
Fabelous Math
Fabelous Math is a simple library designed to provide basic mathematical functions, saving you the trouble of writing these common utilities repeatedly. This library includes essential functions like checking if a number is even or odd.
Installation
You can easily install fabelous-math using pip:
pip install git+https://gitea.fabelous.app/Fabel/fabelous-math.git
Usage
Python
To use the functions provided by Fabelous Math in your Python code, you can import them as follows:
from fabelous_math import is_even, is_odd
# Example usage:
number = 42
print(f"Is {number} even? {is_even(number)}")
print(f"Is {number} odd? {is_odd(number)}")
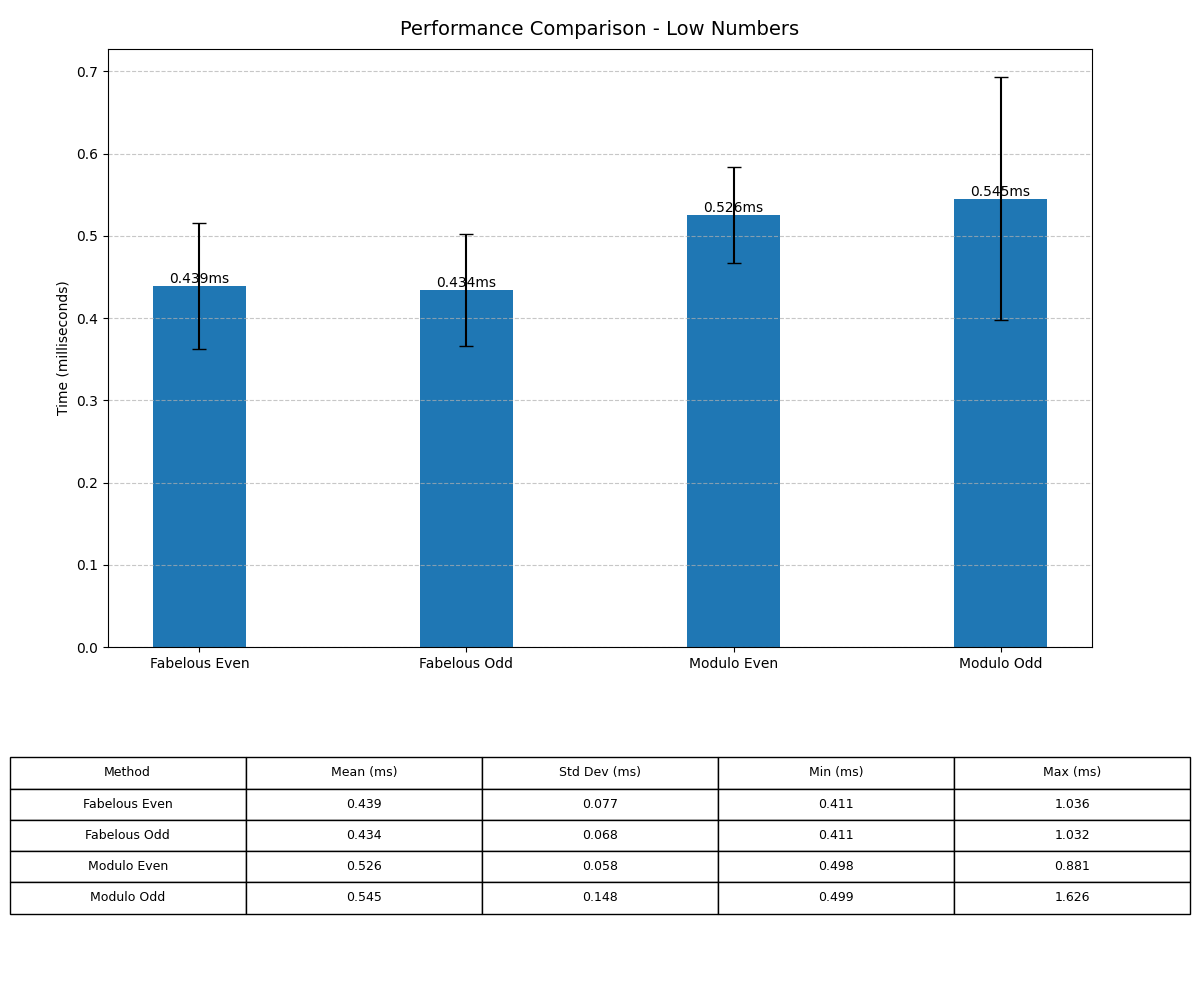
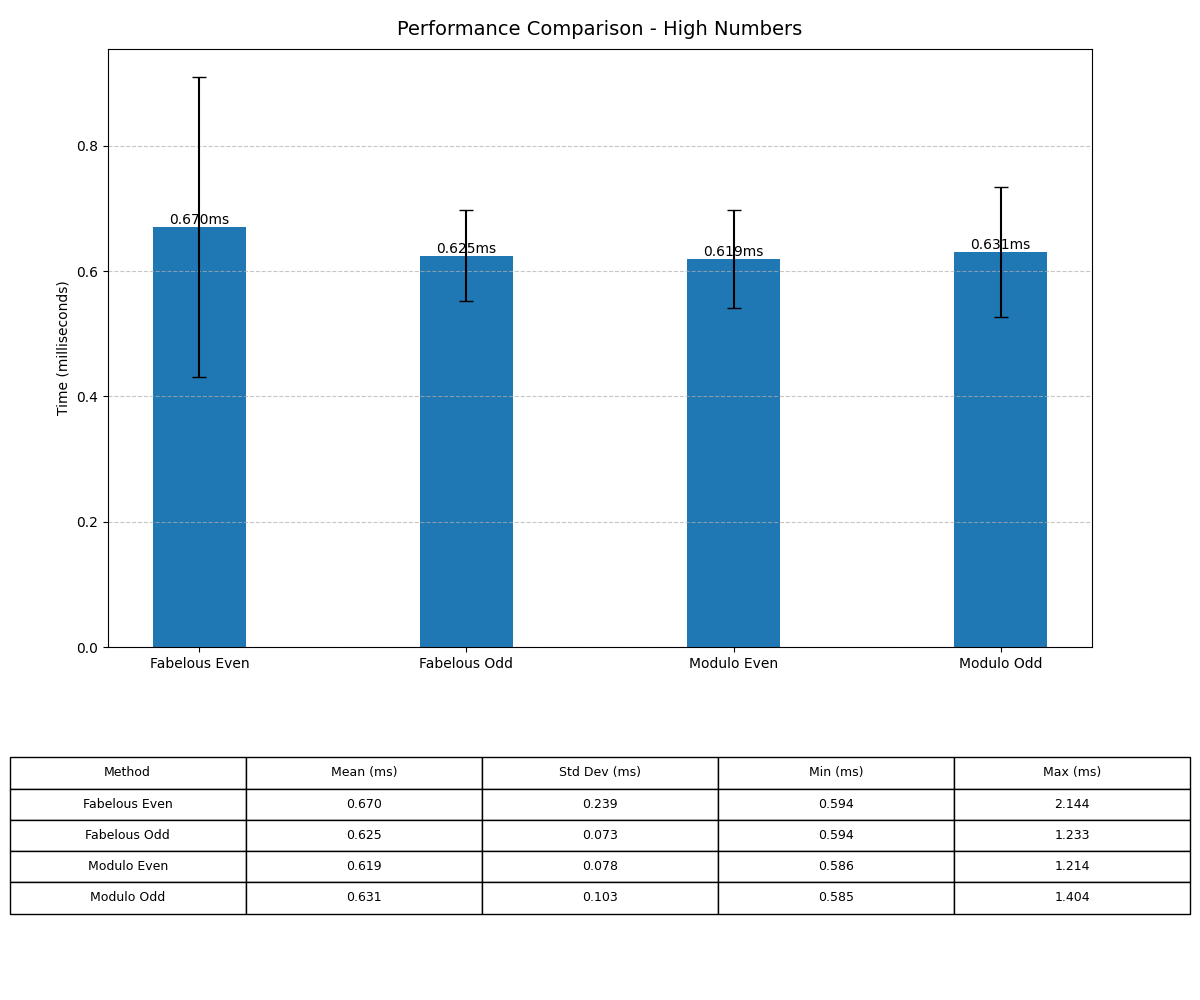
Performance Comparison
To understand the performance of fabelous-math functions, I conducted a series of tests comparing my methods with traditional modulo operations. Below are the results: